Trigonometric substitutions are a specific type of u u u substitutions and rely heavily upon techniques developed for those They use the key relations sin 2 x cos 2 x = 1 \sin^2x \cos^2x = 1 sin2 xcos2 x = 1, tan 2 x 1 = sec 2 x \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and cot I've tried using substitutions for tan or sec, ie tan^2x 1 = sec^2x , but I can't get the answer 32,040 results, page 12 Precalculus check answers help!\sec(2x^{1}1)\tan(2x^{1}1)\times 2x^{11} The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^{n} is nax^{n1} 2\sec(2x^{1}1)\tan(2x^{1}1) Simplify 2\sec(2x1)\tan(2x1) For any term t, t^{1}=t Examples Quadratic equation { x } ^ { 2 } 4 x 5 = 0 x 2 − 4 x − 5 = 0 Trigonometry 4 \sin \theta

Exercise 7 3 Integrals Of The Functions In Exercises 1 To 22 2 Sin 3x Cos 4x 3 Cos 2x Cos 4x Cos 6x 5 Sin X Cos 6 Sin X Sin 2x
Integration of tanx sec^2x root 1-tan^2x
Integration of tanx sec^2x root 1-tan^2x-Integral of tan^2 (x) Integral Calculator Symbolab This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice Geometry betaSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



What Is The Integral Of 1 Sec X Dx Quora
In general Whenever you have an EVEN power of secant, the idea is to "peel off" one sec 2 x and convert all other sec 2 x terms into t a n 2 x 1 terms It's a little annoying to work out the parenthesis on (tan 2Math\int \frac{1\tan^2x}{1\tan^2x} \,dx/math math\int \frac{1\tan^2x}{\sec^2x} \,dx/math math\int \frac{1\tan^2x}{\frac{1}{\cos^2x}} \,dx/math mathDifferentiate c and d, use the product rule to find v Then just use the product rule on u and v 0
I've tried using substitutions for tan or sec, ie tan^2x 1 = sec^2x , but I can't get the answer 31,992 results, page 11 solving trig equations tan(3x) 1 = sec(3x) Thanks, pretend 3x equals x so tanx 1 = secx we know the law that 1 tanx = secx so tanx 1 becomes secx and secx = secx sec(3x) = sec(3x) just put 3x back in for x you don't really have to change 3x to x but itSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
The Second Derivative Of sec^2x To calculate the second derivative of a function, differentiate the first derivative From above, we found that the first derivative of sec^2x = 2sec 2 (x)tan(x) So to find the second derivative of sec^2x, we need to differentiate 2sec 2 (x)tan(x) We can use the product and chain rules, and then simplify to find the derivative of 2sec 2 (x)tan(x) is Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 ta Trig Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan)Integration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help you=> `1 2*tan^2x` It is seen that `sec^4 x tan^4 x = 1 tan^2 x` is not an identity, instead `sec^4x tan^4x = 1 2*tan^2x




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines




The Integral Of Sec 4 X Tan X Mathematics Stack Exchange
By Integr » Tue 531 pm This is a question in the book to integrate by part the following question `int(1tan^2x)/(sec^2x) dx` Can any one help?Thank you Integr Posts 71 Joined Tue 527 pm Top Re how to integrate `int(1tan^2x)/(sec^2x) dx` ?In general if you vave a power of sec or tan youre gonna have to use tan^2x 1 = sec^2x and d/dx(tanx) = sec^2x and d/dx(secx) = secxtanx So not only are sec and tan related by trig they are also related through calculus But practice is important, as you pick up the kinds of techniques to use Yeah, integration is often about learning tricks and gaining experience I would recommend




Sin X 2




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube
Ex 71, 19 sec 2 2 dx sec 2 2 = 1 cos 2 1 sin 2 = 1 cos 2 sin 2 1 = sin 2 cos 2 = tan 2 = sec 2 1 = sec 2Note that once we have a side without an integral on it you need to include a constant of integration I have used $c$ The two expressions on the left hand side are the same so you can add them giving $$3\int \sec^2x \tan^2x dx= tan^2x c$$ So simply divide by 3 to get your answer $$\int \sec^2x \tan^2x dx= \frac{tan^2x}{3} \frac{c}{3}$$This adjustment may work sec x = sec x * (sec x tan x) / (sec x tan x) = g(x) ln (sec x tan x) = integral of g(x)dx So, let u = ln (sec x tan x) du = sec x * sec x tan x / sec x tan x dx integrating u du = u^2/2 = ln (sec x



Solved If Sin2x 3 5 Find All Possible Values Of Sin X Tan X Cos X Cot X Sec X Csc X If Cosx 3 5 Find All Possible Values Of Sin2x Tan2x Course Hero
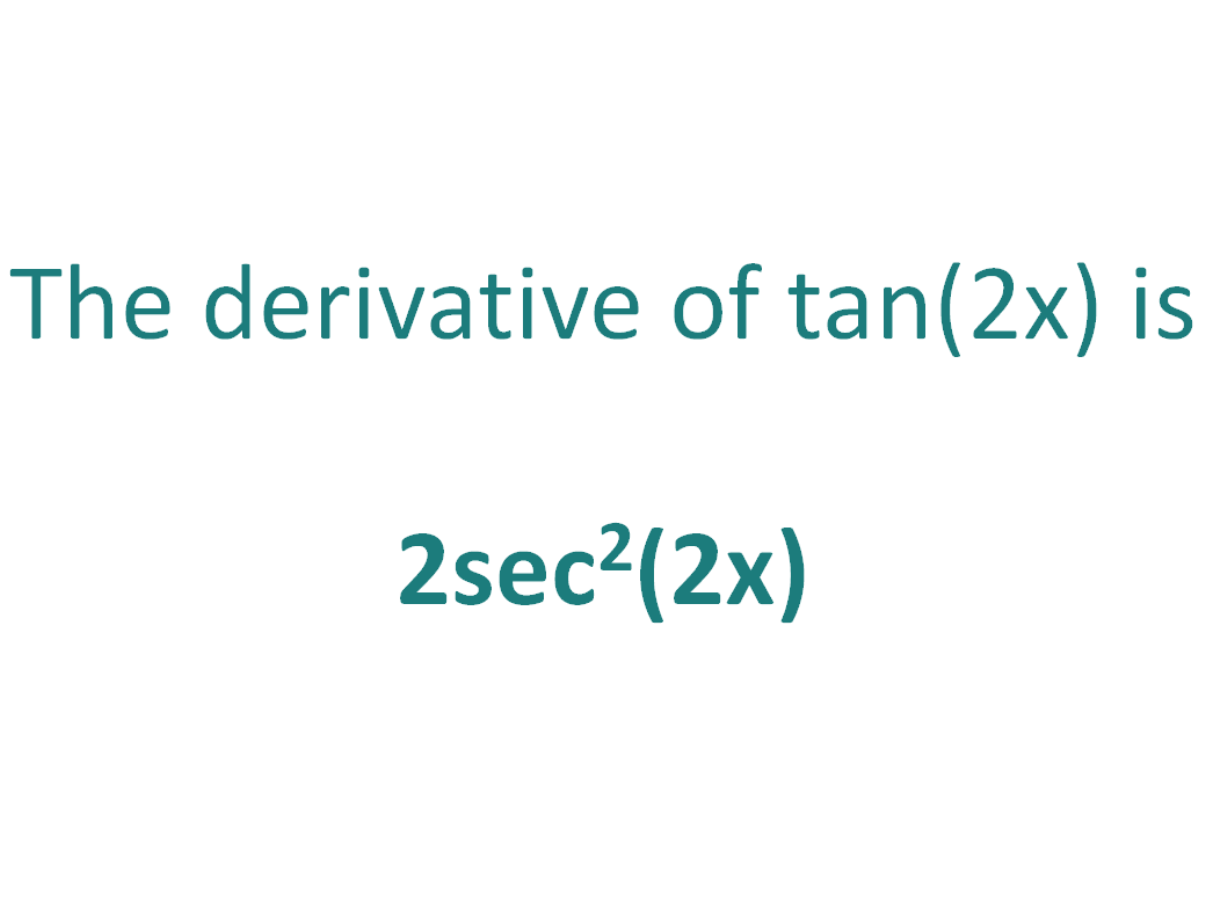



The Derivative Of Tan 2x Derivativeit
Answer to Evaluate the integral using the substitution rule (Use C for the constant of integration) 1 sec (2x) tan(2x) dx Tutori Calculus 2, integral of (1 tan^2x) sec^2x, integral of cos(2x) Hi simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2click here👆to get an answer to your question ️ if sec x sec^ 2x = 1 then the value of tan^ 8 tan^ 4 2tan^ 2x 1 will be equal tox = 1287 2 = the period of the function is the Ex 76, 24 ∫1 𝑒^𝑥 sec𝑥 (1tan𝑥 )𝑑𝑥 "ex" cos x C (B) "ex" sec x C "ex" sin x C (D) 𝑒𝑥 tan x C ∫1 𝑒^𝑥 sec𝑥 (1tan𝑥 )𝑑𝑥 = ∫1 𝑒^𝑥 (sec𝑥sec𝑥 tan𝑥 )𝑑𝑥 It is of the form ∫1 〖𝑒^𝑥 𝑓(𝑥)𝑓^′ (𝑥) 〗 𝑑𝑥=𝑒^𝑥 𝑓(𝑥)𝐶 Where 𝑓(𝑥)=sec𝑥




Int Dx Sec 2xtan 2x




Integration Calculus Notes
Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx Calculus Solve The posistion of a particle moving along a coordinate line is s=sqrt(54t), with s in meters and t in seconds Find the particle's velocity at t=1 sec A) 2/3 m/sec B) 4/3 m/sec C) 1/3 m/sec D) 1/6 m/sec Thank you! To integrate \(\displaystyle ∫\tan^kx\sec^jx\,dx,\) use the following strategies 1 If \(j\) is even and \(j≥2,\) rewrite \(\sec^jx=\sec^{j−2}x\sec^2x\) and use \(\sec^2x=\tan^2x1\) to rewrite \(\sec^{j−2}x\) in terms of \(\tan x\) Let \(u=\tan x\) and \(du=\sec^2x\) 2 If \(k\) is odd and \(j≥1\), rewrite \(\tan^kx\sec^jx=\tan^{k−1}x\sec^{j−1}x\sec x\tan x\) and use \(\tan^2x=\sec^2x−1\) to Integral of (tan^3x xtan^2x)dx here's your answer integrate the following wrt x (tan3x xtan2x) ∫tan3x xtan2x dx Integral (tan 2x sec 2x)2 julianairma78 julianairma78 matematika sekolah menengah atas dapatkan app brainly unduh app ios Integral (tan^2x sec^2x) (1 tan^6x)dx get the answers you need, now!




Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Math Videos Maths Exam Calculus



Integral Sec2x Tan2x Dx Youtube
22 Integrals of Trigonometric functions Integrals of the form ∫ sin ( m x) sin ( n x) d x, ∫ cos ( m x) cos ( n x) d x, and ∫ sin ( m x) cos ( n x) d x Integrals of the form ∫ tan m x sec n x d x Functions involving trigonometric functions are useful asIntegration is an important tool in calculus that can give an antiderivative or represent area under a curve The indefinite integral of , denoted , is defined to be the antiderivative of In other words, the derivative of is Since the derivative of a constant is 0, indefinite integrals are defined only up to an arbitrary constant For example, , since the derivative of is The definiteIntegral of sec^2x \square!




Int 3 Tan 2x 2 Sec 2x Tan 3x 2tanx 5 2dx




Ppt 7 2 Trigonometric Integrals Powerpoint Presentation Free Download Id
Integration of sec^2x ÷cosec^2x dx 1 See answer deeksha18 is waiting for your help Add your answer and earn points Brainly User Brainly User We know 1/sec^2x = cos^2x And 1/cosec^2x= sin^2x So will integrating we will left with, tan^2x= sec^2x11) Find an expression equivalent to sec theta sin theta cot theta csc theta tan theta csc theta sec theta ~ sin theta 2) Find an expression equivalent to cos theta/sin theta tan theta cot theta ~ sec theta csc theta 3) Simplify (tan how to integrate `int(1tan^2x)/(sec^2x) dx` ?




Vi Evaluate The Indefinite Integ 1 T Se Gauthmath



2
Integration Trig identities ppt download if `f((2tanx)/(1tan^2x))=((cos2x1)(sec^2xtanx))/2` then `f(x)=` Solved Find The Derivative Of The Function Y = 3/5 Sec^2 Answered x² d Find dx (e" tant)dt tan(x?) a bartleby Solved Find The Derivative 7) F(x) = Sin' 2x/cos 2x 8) F Math 1A — UCB, Spring 10 How to calculate the derivative of sec^2 x Quora IntegrateI got $\ln\sec(2x 1) \tan(2x1) \text C$ as an answer I saw that the integral of $\sec x$ is $\ln\sec x \tan x \text C$ But I feel I may have left something out because that was too easyGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Www Assignmentexpert Com Homework Answers Mathematics Answer Pdf
Integration of sec^2x/(secx tanx)^n Functions involving trigonometric functions are useful as they are good at describing periodic behavior This section describes several techniques for finding antiderivatives of certain combinations of trigonometric functions In learning the technique of Substitution, we saw the integral \(\int \sin x\cos x\ dx\) in Example 614 The integration wasUse the half angle formula to rewrite cos2(x) cos 2 ( x) as 1cos(2x) 2 1 cos ( 2 x) 2 Since 1 2 1 2 is constant with respect to x x, move 1 2 1 2 out of the integral Split the single integral into multiple integrals Since 1 1 is constant with respect to x x, move 1Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Integral Of Cos 2x Tan 4x




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit
Consider the integral $$\int \sec^4(x)\tan(x)$$ Now right off the bat I see two ways of solving this Let u= $\sec(x)$ 2Use integration by parts Now doing the first way results in the integrand looking like $$\int u^3du=\frac{1}{4}\sec^4(x)C $$ Which is correct but it's not the answer I'm looking for, so instead we'll do it the second wayQuestion Please help me verify this equation cscx cscx =2sec^2x 1cscx 1cscx yes, the cscx's are over 1cscx and 1cscx Those are fractions So far i have gotten stuck onAnyways I looked at the solutions manual and they magic out $$1 \tan x \tan 2x = 1\tan x\left(\frac{2 \tan x}{1\tan ^2x}\right) $$ which I recognize as the double angle forumla sort of, I just don't understand why I can use that and how they magiced it into this It is just too difficult to think of an equation in an equation in an equation I tried working with this and got nowhere near




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Integration Calculus Notes
1/2 (2xsin (2x)) x C Using the following relation, \tan ^2x\=1\sec ^2x int (11sec^2(x))/sec^2(x)dx Applying sum rule, int f(x) g(x) dx=int f(x)dx intg(x) dx \int \frac{1}{sec ^2x)dx\int \frac{1}{\sec ^2(x\)}dx\int \frac{\sec ^2(x\)}{\sec ^2(x\)}dx eq(i) \int \frac{1}{\sec ^2(x\)}dx=\frac{1}{4}(2x\sin (2x)) \int \frac{1}{\sec ^2(x\)}dx=\frac{1}{4}(2x\sin (2x)) \intAnswer to How to integrate 1/(sec(x)^2) By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask`(tan 2x)/(1 sec 2x) = tan x``("sin x cos x")^(2) =1 sin 2x ` About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new




Evaluate The Following Integral Sec 2x Tan 2x Dx Sec Chegg Com



8 T Tan 2x Cot 2 X 1dx 9 T Frac 1 Cos Gauthmath
The following is a list of integrals (antiderivative functions) of trigonometric functionsFor antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functionsFor a complete list of antiderivative functions, see Lists of integralsFor the special antiderivatives involving trigonometric functions, see Trigonometric integralBecause 1/2 is a constant, we can remove it from the integration to make the calculation simpler We are now integrating 1/2 x ∫(1 cos(2X)) dX = 1/2 x (X 1/2sin(2X)) C It is very important that as this is not a definite integral, we must add the constant C at the end of the integration Simplifying the above equation gives us a final answer ∫sin 2 (X) dX = 1/2X 1/4sin(2X) CKeep breaking it down until you find something you can work with Let u=sec^2 and v=tan^2 and if that's still too much at this stage Let a=sec b=sec c=tan d=tan Differentiate a and b, use the product rule to find u;




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




Find Integral X 2 Sin 2 X Sec 2 X 1 X 2 Teachoo
Prove that cot x tan 2x1 =sec 2x calc Use the graph of f(t) = 2t 4 on the interval −4, 6 to write the function F(x), where f of x equals the integral from 2 to x of f of t dt Calculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x) About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How worksBy barnamah » Tue 801 pm Here is



Q Tbn And9gcr1hzoptmtla Kxxcxtkksx7s8mu4uts6 74qmdsrnv4xuqmwwt Usqp Cau




Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x




Lim X Tends To Pi 4 Sec 2x 2 Tanx 1 Brainly In




Examples Int Tan 2x Sec 4x Dx




Int Tan 2x Secx 1 Dx Youtube



3
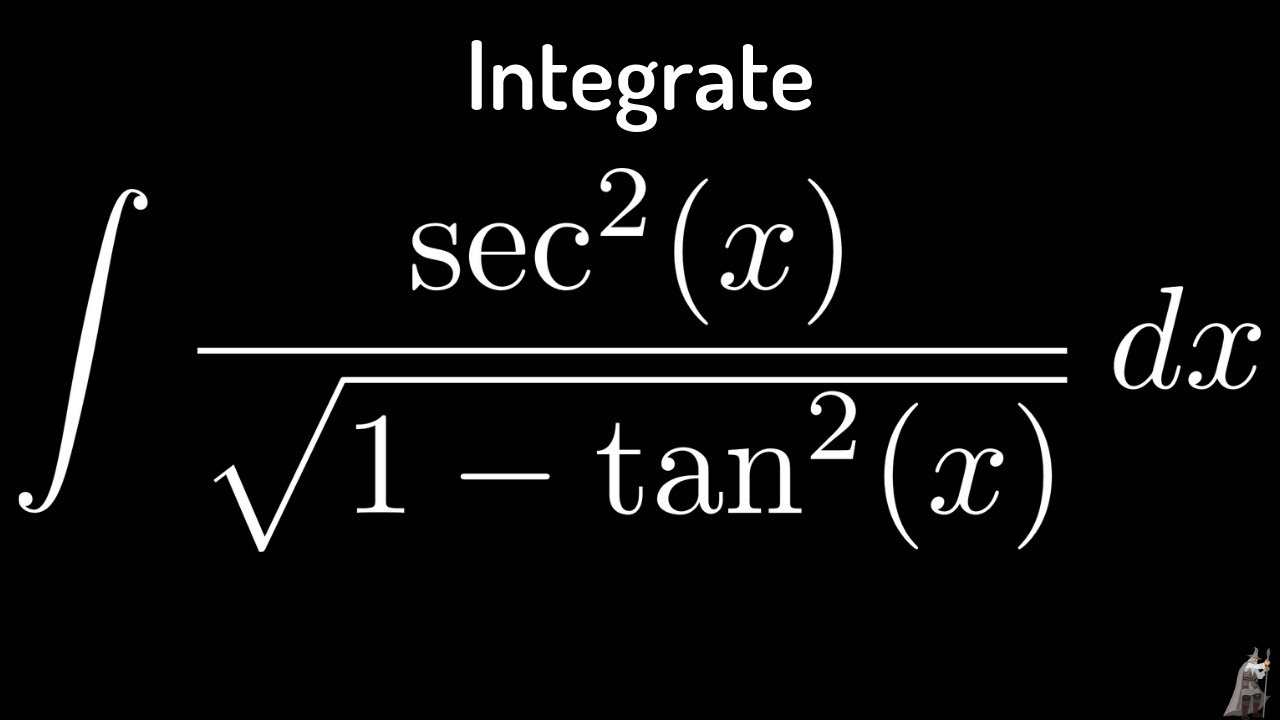



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube



1




Answered 52 Csc X Cscx Dx Tan 2x Tan 2x Bartleby




D Integral 2 Pdf Sine Trigonometric Functions




Integrate 4x Csc 2 X 2 5 Dx Integrate X 1 Sec Chegg Com




Evaluate Int 0 Pi 4tan 3xsecxdx




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange




Find Integral X 2 Sin 2 X Sec 2 X 1 X 2 Teachoo




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




Separable Differential Equation Csc Y Dx Sec 2 X Dy 0 Differential Equations Math Videos Equation




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Powers Of Trigonometric Functions




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube




Integral Sec 4 X Tan 3 X Dx Integral Tan 4 2x Dx Chegg Com




Tan2x Sec2x ただの悪魔の画像




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Strategy For Integration By Parts




Integration Trig Identities Ppt Download




Int Tan 2xsec 2x 1 Tan 6x Dx
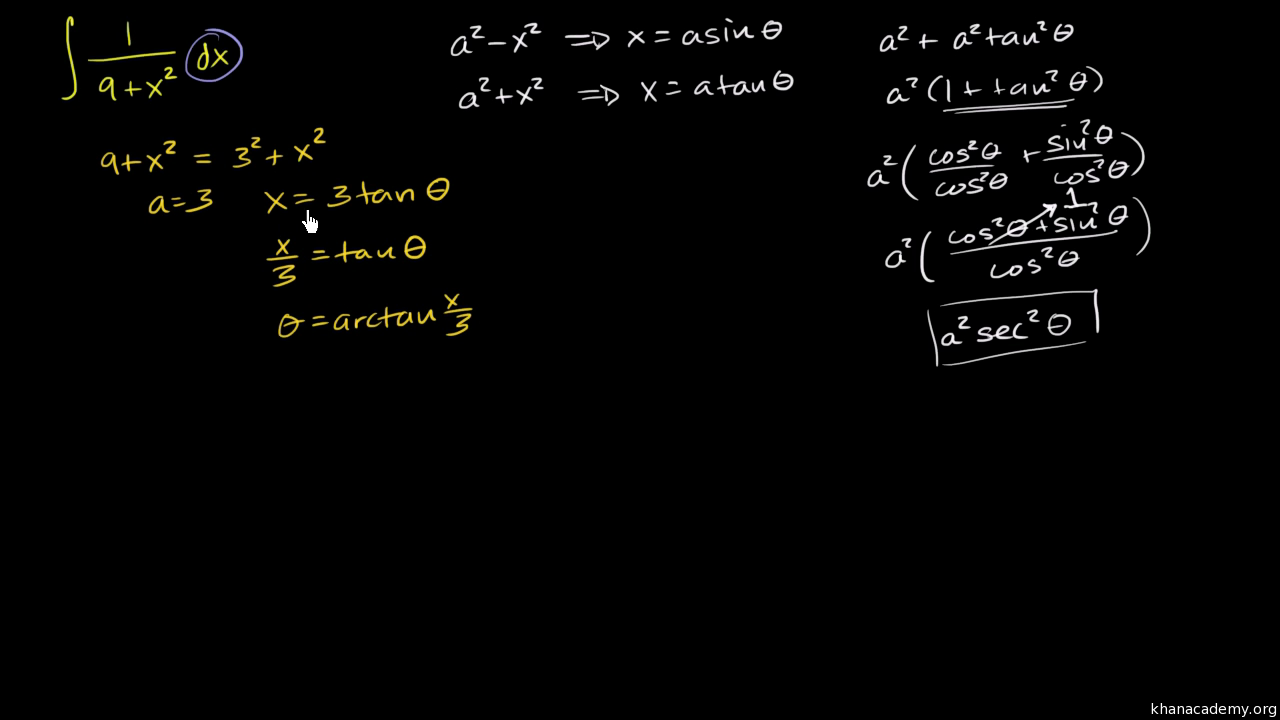



Trig Substitution With Tangent Video Khan Academy




Tan2x Sec2x ただの悪魔の画像




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Integration Trig Identities Ppt Download




How Do You Integrate 1 Tan2x Sec2x Dx Socratic




Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12




Integral 1 Tan 2 X Sec 2 X Youtube




Question 1 Integrate The Following Function Sec 2x Chegg Com




How Do You Evaluate The Integral 1 Tan X 3 Sec 2 X Dx Within The Range 0 Pi 4 Socratic




Integration Trig Identities Ppt Download




Int Tan 2xsec 2x 1 Tan 6x Dx Youtube




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians



Http Www Math Ncku Edu Tw Rchen 18 19 teaching Chapter 7 Stewartcalc8 07 02 Pdf




Integration Trig Identities Ppt Download




Given T Tan 2x Sec 4xdx Which Of The Fol Gauthmath



What Is The Integral Of 1 Sec X Dx Quora




Integration Of Tan 2 X Sec 2 X Youtube




Int Tanx Sec 2 X 1 Tan 2 X Dx




Integral Sec N X Dx 1 N Minus 1 Sec Nminus 2 X Tan Chegg Com



Indefinite Integration Integral Calculus Maths Solved Objective Problems For Iit Jee Mains Advanced A1 Maths




If Y Tan X Tan 2x Tan 3x Then Dy Dx Equals



1




Trigonometric Integrals Powers Of Secant And Tangent Sec 4 2x Tan 4 2x Math Videos Maths Exam Calculus




How Do You Integrate Int Sec 1 X Tan 1 X Dx Socratic




Ex 7 6 24 Integrate E X Sec X 1 Tan X Dx Is A E X Cos X



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 6 Pdf




Int 0 Pi 3 Secxtanx 1 Sec 2x Dx




Integration Sec 2x Cosec 4x Brainly In




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




1 Tanx Tan X 2 Secx Tanx Cotx 2 1 Prove It Brainly In
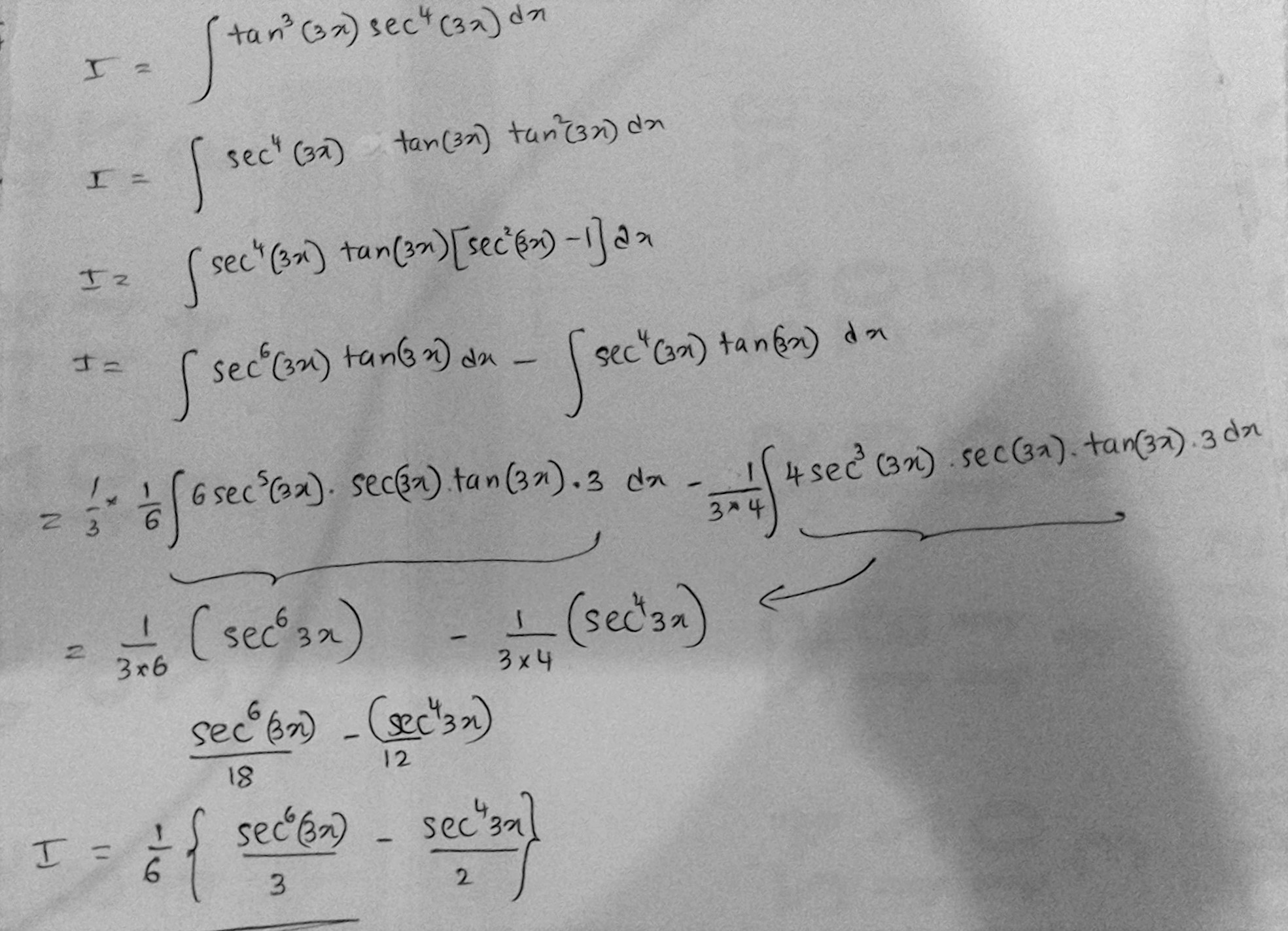



Find Integration Of Tan 3 3x Sec 4 3x Dx Socratic




Given T Tan 2x Sec 4xdx Which Of The Fo Gauthmath




Trig Identity Sec2x Minus Tan2x T10 Youtube



Http Www Ppup Ac In Download Econtent Pdf B sc Math part1 paper 2 Pdf




Evaluate Int Sec 2xtanx Sec 2x Tan 2x Dx




Integral Of Frac Sec 2 X Tan X Sec 2 X Tan X Mathematics Stack Exchange



2




Integration Calculus Notes




Exercise 7 3 Integrals Of The Functions In Exercises 1 To 22 2 Sin 3x Cos 4x 3 Cos 2x Cos 4x Cos 6x 5 Sin X Cos 6 Sin X Sin 2x
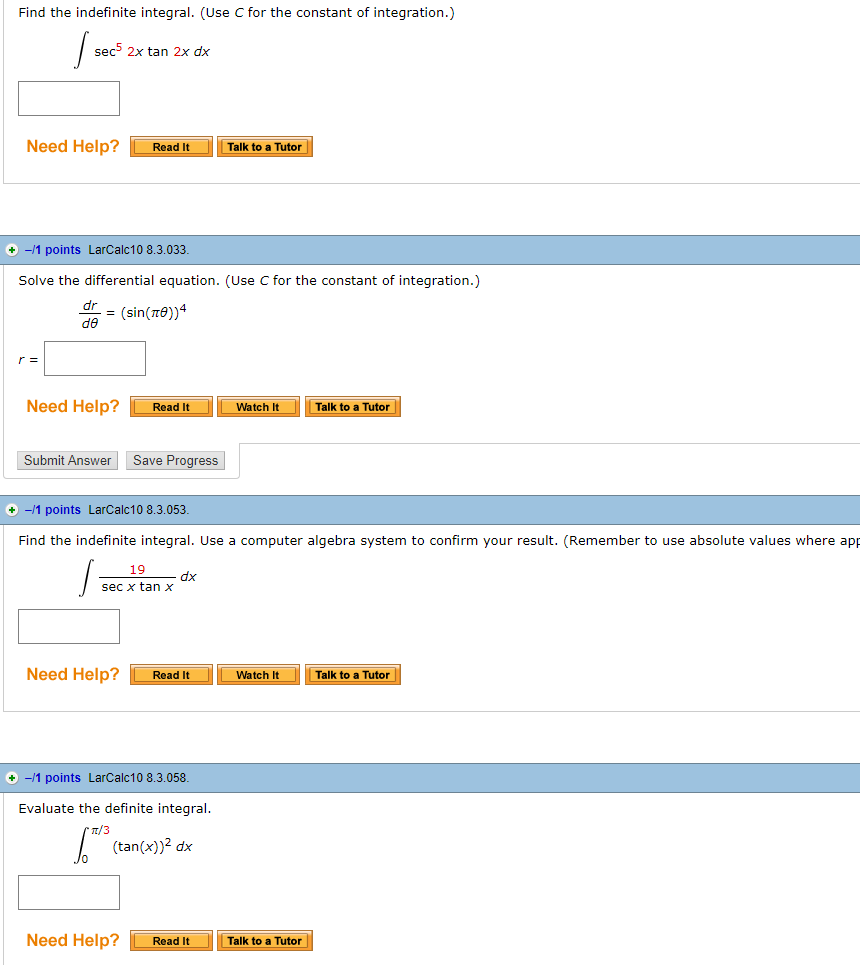



Find The Indefinite Integral Use C For The Constant Chegg Com




Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12




Solve Diff Equation Dy Dx Y Sec 2 X Tan X Sec 2x Brainly In



What Is The Integration Of 1 2tanx Tanx Secx 1 2 Dx Quora




Sec 2 2x 1 Tan2x Youtube
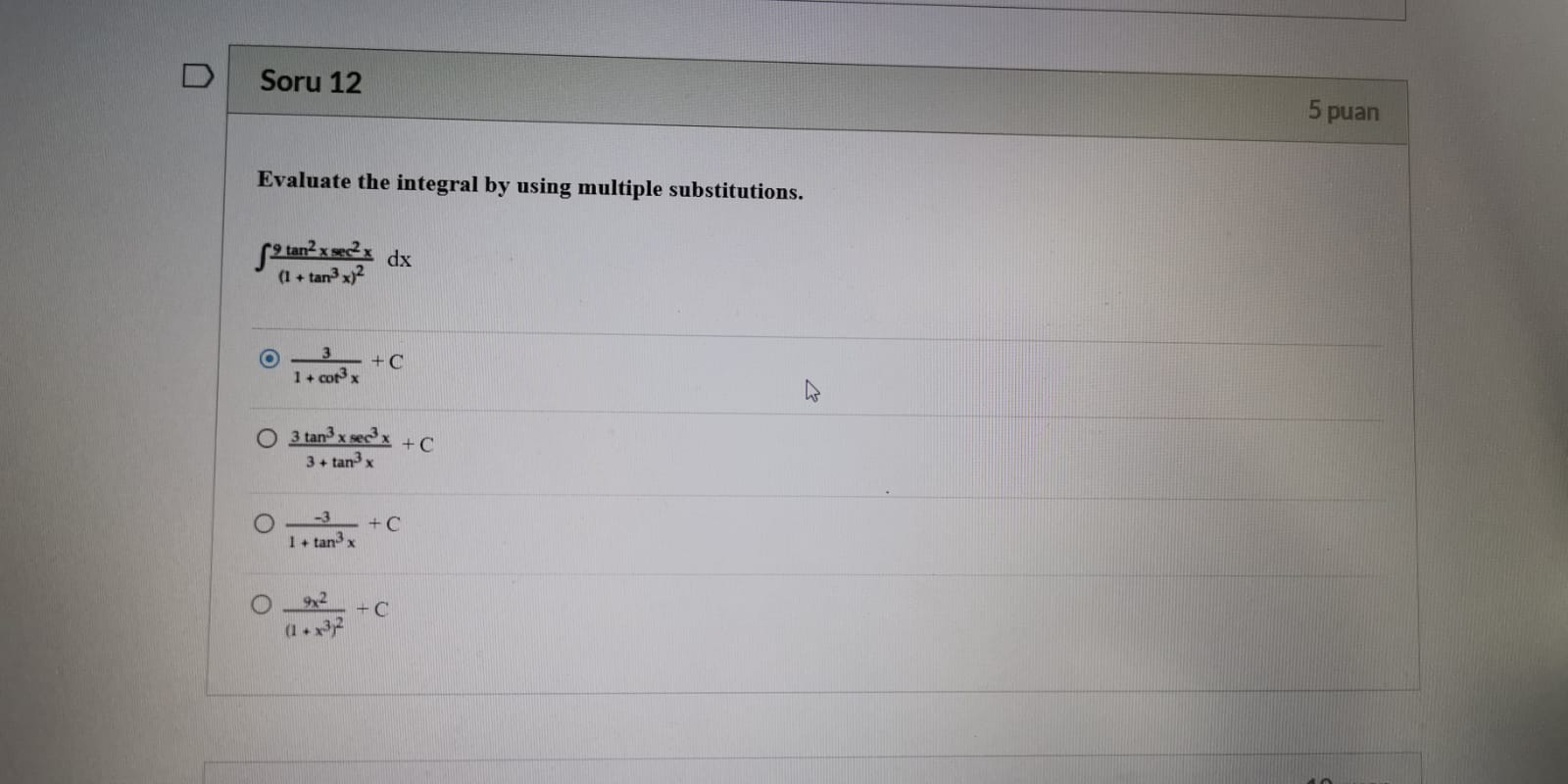



Answered Evaluate The Integral By Using Multiple Bartleby



What Is The Integral Of 1 Secx Cosecx Quora




Fundamental Theorem Of Calculus Part
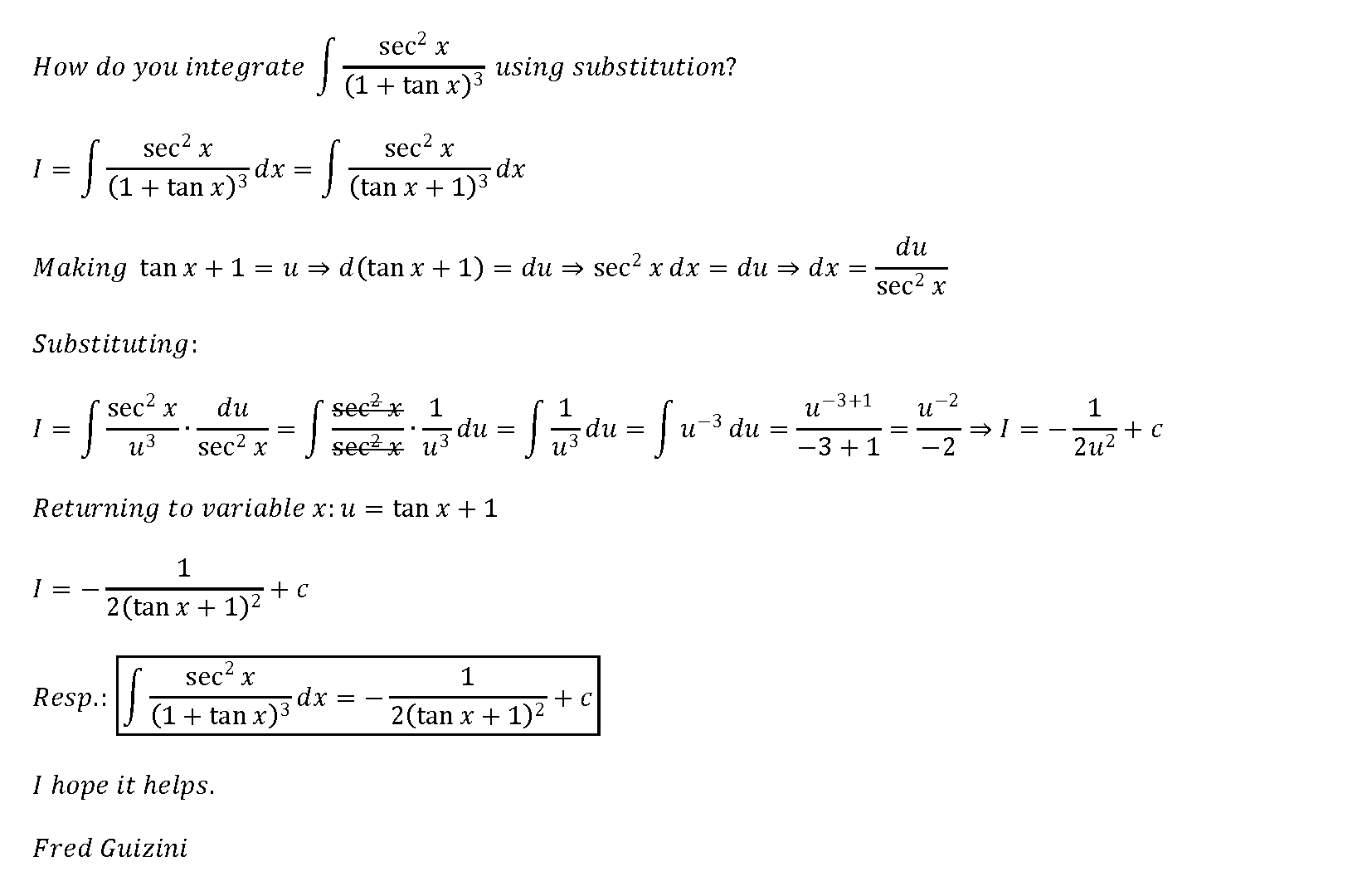



How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic




Tan2x Sec2x ただの悪魔の画像




C4 Chapter 6 Integration Ppt Download




Integral Evaluation Mathematics Statistics And Calculus Solution Manual Docsity




Answered Evaluate The Integral 5 Sin X 8 Sec X Bartleby
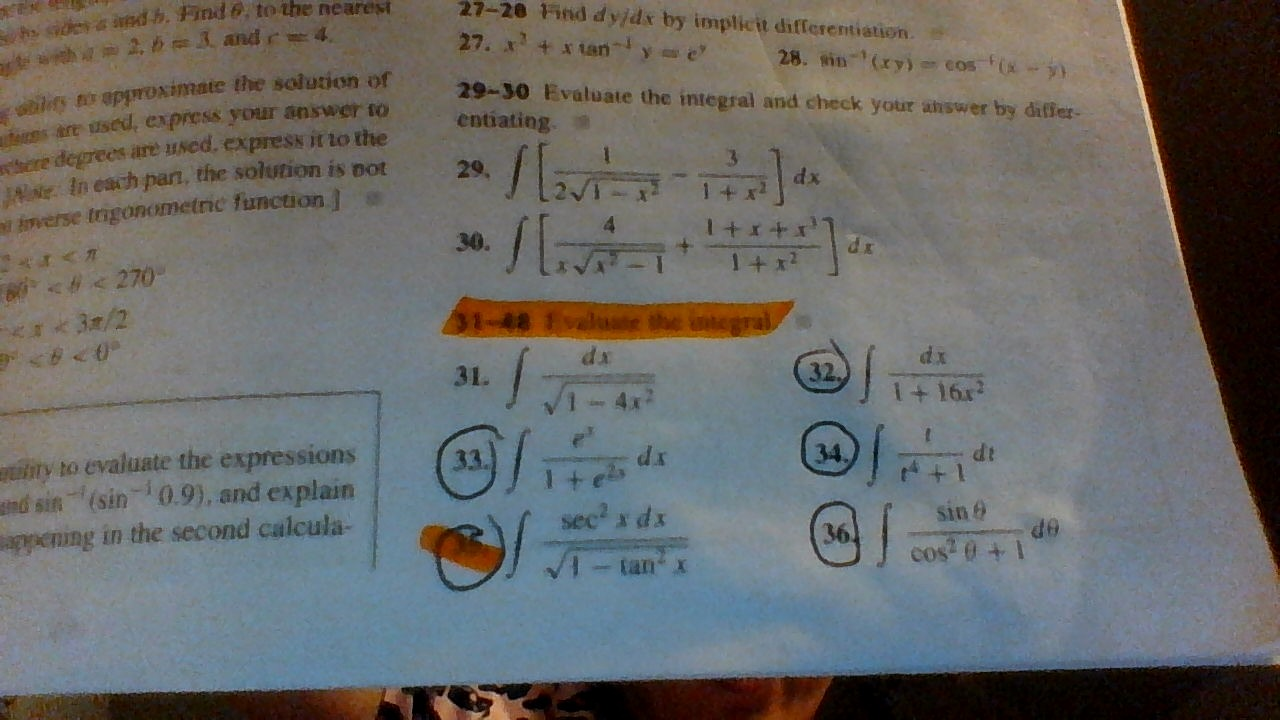



Evaluate The Integrals Dx 1 16x 2 E X 1 E 2x T Chegg Com



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 6 Pdf



0 件のコメント:
コメントを投稿